Lean Is Mean

Before its billion-dollar acquisition by Facebook in 2012, Instagram had a team of only 13 employees. WhatsApp, acquired two years later for $19 billion, had just 55. Airbnb and Stripe, both founded at a similar time, are notorious for having gone to extreme lengths to hire only exceptional people and rarely did so in their early years.

What has caused us to forget the ancient wisdom of the early 2010s? Unironically, a fear of being trapped in the permanent underclass. An unprecedented urgency to not be left behind. If you talk to founders in 2025, even early-stage ones, many of them will describe their market as a "land grab". Particularly in fast-moving areas like applied AI, data, and infrastructure, a widespread belief is that there is a short window of opportunity to gain a foothold and establish prohibitive dominance or face being boxed out. I would characterize this as a period of industry-wide blitzscaling, wherein most founders have decided it is necessary to throw themselves off the cliff and assemble their airplanes on the way down.

Why Stay Lean?

Investors and entrepreneurs from Sam Altman to Andrej Karpathy have articulated the importance of staying lean in an intuitive way. These arguments tend to emphasize the psychological and cultural benefits of a small team. But I want to make the case here that the problems caused by scaling the workforce of a startup can be rigorously modeled, and that psychology and culture are downstream of that. This can be done regardless of the nuances of who constitutes the company, in much the same way that neural scaling laws are robust to architectural and algorithmic variation.

I make three arguments for scaling slowly. The first is against a fast growth rate, with the assumption that hiring more quickly necessitates lowering the bar for quality. The next two are arguments against size itself: the economic inefficiencies of scale and the inherent incentive misalignments.

Speed vs Selectivity

No one espouses the value of preserving the quality of early hiring decisions more than Paul Graham. He famously discusses it in How to Make Wealth, declaring: "Steve Jobs once said that the success or failure of a startup depends on the first ten employees. I agree. If anything, it's more like the first five." His acolytes, YC founders like Patrick Collison, Brian Chesky, and Alexandr Wang have each demonstrated this belief.

Intuition

The core premise is that hiring decisions, more than decisions of any other type, compound over time. Engineers are only able to recruit, vet, and train talent at or perhaps slightly above their own level of expertise, willpower, and intelligence. Thus, early hires set the tone for all subsequent hiring decisions.

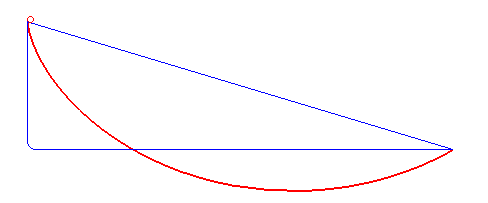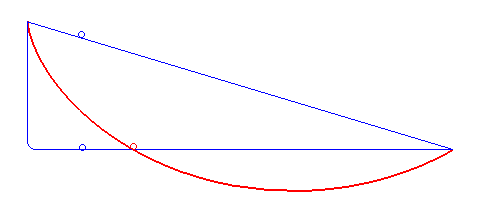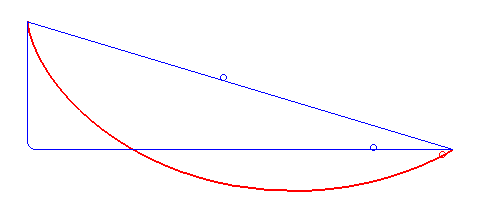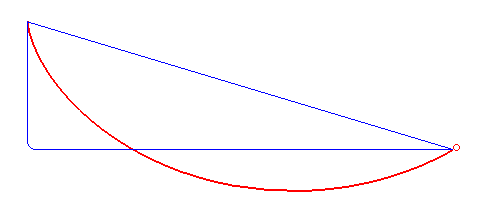
My preferred analogy for selective hiring is the brachistochrone problem, where you are tasked with finding a curve which will minimize the time it takes to travel from one point to another. The solution is a cycloid, not a straight line. Even though the cycloid is longer, it reaches the endpoint faster because it front-loads acceleration — it descends steeply at first, trading distance for speed that compounds later.

Under reasonable modeling assumptions, an optimal hiring policy might exhibit a similar kind of property—where front-loading selectivity yields faster overall progress toward scale, even when constrained by baseline quality. Michael Truell expressed such thoughts in a YC interview: "So we agonized over the first hires. And I think that if you want to go fast on the order of years, actually going slow on the order of 6 months is super helpful".

Model

Consider a model of sequential hiring where, at each step $i > 0$, we can invest a positive amount $x_i$ (representing time or attention) to improve the quality of the next hire. The realized quality of hire $q_i$ depends both on the direct investment $x_i$ and the average quality of all previous hires:

$$q_i = x_i + \frac{1}{i}\sum_{j=0}^{i-1} q_j - d, \quad q_0 = 0,$$

where $d > 0$ is a constant drag term capturing baseline difficulty or fatigue.
We seek to minimize the total cost of investments subject to a balance constraint on total quality:

$$\min_{x_1, \dots, x_n > 0} \sum_{i=1}^{n} f(x_i) \quad \text{subject to} \quad \sum_{i=0}^{n} q_i = 0,$$

where $f$ is a differentiable, strictly convex cost function.

Define the cumulative quality $S_i = \sum_{j=0}^{i} q_j$. From the recurrence relation,

$$S_i = S_{i-1} + q_i = \Big(1 + \frac{1}{i}\Big) S_{i-1} + x_i - d,$$

and unrolling with $S_0 = 0$ yields

$$S_n = \sum_{i=1}^{n} (x_i - d)\prod_{t=i+1}^{n}\Big(1 + \frac{1}{t}\Big) = (n+1)\sum_{i=1}^{n} \frac{x_i - d}{i+1}.$$

The constraint $S_n = 0$ therefore becomes

$$\sum_{i=1}^{n} \frac{x_i}{i+1} = d \sum_{i=1}^{n} \frac{1}{i+1}.$$

This is a linear constraint of the form

$$\sum_{i=1}^{n} w_i x_i = C, \quad\text{where}\quad w_i = \frac{1}{i+1}, \;\; C = d\sum_{i=1}^{n} \frac{1}{i+1}.$$

The optimization problem is

$$\min_{x_i>0} \sum_{i=1}^{n} f(x_i) \quad\text{s.t.}\quad \sum_{i=1}^{n} w_i x_i = C.$$

Forming the Lagrangian

$$\mathcal{L}(x, \lambda) = \sum_{i=1}^{n} f(x_i) + \lambda \Big(\sum_{i=1}^{n} w_i x_i - C\Big),$$

and taking first-order conditions gives

$$f'(x_i) + \lambda w_i = 0 \quad\Rightarrow\quad x_i = (f')^{-1}(-\lambda w_i).$$

Since $f$ is strictly convex, $f'$ is strictly increasing and its inverse $(f')^{-1}$ is also strictly increasing.
Because $w_i = 1/(i+1)$ is strictly decreasing in $i$, it follows that

$$w_1 > w_2 > \cdots > w_n \quad\Rightarrow\quad x_1 > x_2 > \cdots > x_n.$$

Hence, for any differentiable, strictly convex $f$, the optimal investments $x_i$ are strictly decreasing in $i$. In other words, for a simple model of sequential hiring where you have to expend effort to improve the quality of the next hire relative to the existing team, you are best served by investing the most time in your earliest hires.

Diseconomies of Scale

The first category of issues posed by scale itself is the set of operational inefficiencies that cause a drop in the per-capita productive output of the team. That is to say, even hiring exceptional and highly motivated employees, there is an inevitable coordination cost and strategic disadvantage to scale. These effects necessarily occur in the context of a rising burn rate, a burn rate that likely does not rise sub-linearly due to the combination of pay raises and wage compression.

Coordination Scales Quadratically

Pairwise interactions between team members grow roughly quadratically as a function of team size ($O(n^2)$):

$$f(n) = {n \choose 2} = \frac{n(n-1)}{2}.$$

This corresponds to everything from communication cost to duplication of effort to decision-making overhead. It is observable in technical areas like merge conflicts in a codebase and personnel areas like human resources complaints. The natural solution to this is to preserve smaller teams, capping them at some reasonable size $k$ and introducing a hierarchy in order to maintain centralized decision-making.

Hierarchy Is Logarithmic

Problem solved, right? We now incur those costs proportional only to $k$. But we've introduced new sources of inefficiency. The organization has layers of management, growing proportional to $\log_k(n)$. This results in "top-heaviness" which incurs a relative cost of $\frac{1}{k+1}$. More importantly, leadership is now distant from productive output by $\log_k(n)$ layers, leading to a lack of visibility and organizational inertia. That delay propagates through feedback up the chain and decision-making down.

Game-Theoretic Considerations

Operational inefficiencies are not the only issue caused by scale. It is unrealistic to assume that teams operate as perfectly cooperative collectives; organizations are better modeled as systems of interacting agents whose objectives only partly align. This poses a variety of principal-agent problems which affect how much and where employees concentrate effort, a few of which I discuss here (I omit some, e.g. penalizing difficult to measure tasks).

Free Riding

One of the defining characteristics of startups is employee ownership, which aligns incentives between employees and the company. The most obvious negative effect of scale is that it dilutes the marginal return to effort, causing employees to work less. Suppose there are $n$ risk-neutral employees. Each employee $i$ chooses effort $e_i \ge 0$ with personal cost $c(e_i)$, where $c'(e) > 0$ and $c''(e) > 0$. Individual output contributions follow a concave function $f(e_i)$; only aggregate output is observable:

$$Y = \sum_{i=1}^n f(e_i) + \varepsilon, \qquad \mathbb{E}[\varepsilon] = 0,\ f'(e) > 0,\ f''(e) \le 0.$$

Each employee is compensated by a linear sharing rule:

$$w_i = a + bY, \qquad 0 \le b \le 1,$$

where $b$ is the employee’s share of total output (equity) and $a$ is a fixed component (salary). Employee $i$’s expected utility is

$$U_i = a + b\,\mathbb{E}[Y] - c(e_i).$$

Given the effort levels of the other employees, employee $i$ chooses $e_i$ to maximize expected utility. The first-order condition is

$$b\,f'(e_i) - c'(e_i) = 0.$$

In a symmetric equilibrium ($e_i = e$ for all $i$),

$$c'(e) = b\,f'(e).$$

If everyone could coordinate to maximize total output minus total cost, the efficient effort level $e^{\mathrm{opt}}$ solves

$$\max_e \; n f(e) - n c(e) \quad \Rightarrow \quad f'(e^{\mathrm{opt}}) = c'(e^{\mathrm{opt}}).$$

Under equal sharing, $b = 1/n$, the equilibrium condition becomes

$$c'(e^*) = \frac{1}{n}\,f'(e^*),$$

so $e^* < e^{\mathrm{opt}}$. Since $f'(e)$ is decreasing and $c'(e)$ increasing, this implies $\frac{de^*}{dn} < 0$: equilibrium effort falls as group size $n$ rises because each employee’s marginal return to effort is diluted by the factor $1/n$.

Really there are two phenomena at play here as the team grows: employees necessarily own a smaller share of the output itself and the return to effort for the company decreases. The latter effect implies that bringing in new employees can even reduce output of existing ones.

Rent-Seeking

We showed that when a company cannot view the effort of an individual employee, effort drops. But if we suppose that companies can view effort noisily, we'll see that effort is not only reduced absolutely by scale, but also misallocated towards collectively unproductive activities, like politicking and influence-seeking. Take the earlier model, but now assume effort is split between

• production $e_i^p \ge 0$ (produces output for the company), and
• influence $e_i^r \ge 0$ (increases internal standing).

Effort cost is still convex in the sum: $c(e_i^p + e_i^r)$ with $c'>0$, $c''>0$.

True output depends only on productive effort:

$$Y \;=\; \sum_{i=1}^n f(e_i^p) + \varepsilon, \qquad \mathbb{E}[\varepsilon]=0,\; f'>0,\; f''\le 0.$$

The company cannot observe $e_i^p$ or $e_i^r$ directly. It observes a noisy individual score

$$y_i = f(e_i^p) + g(e_i^r) + \eta_i, \qquad \mathbb{E}[\eta_i] = 0,\ g'(e) > 0,\ g''(e) \le 0,$$

and uses the relative component

$$s_i = y_i - \bar{y}, \qquad \bar{y} = \frac{1}{n}\sum_{j=1}^n y_j,$$

to rank employees.

Compensation depends on total output and relative standing:

$$w_i = a + bY + \beta s_i, \qquad 0 \le b \le 1,\ \beta \ge 0.$$

Each employee chooses $(e_i^p, e_i^r)$ to maximize expected utility:

$$U_i = \mathbb{E}[w_i] - c(e_i^p + e_i^r).$$

The first-order conditions are

$$b\,f'(e_i^p) + \beta\,\frac{\partial s_i}{\partial e_i^p} = c'(e_i^p + e_i^r),$$ $$\beta\,\frac{\partial s_i}{\partial e_i^r} = c'(e_i^p + e_i^r).$$

In symmetric equilibrium ($e_i^p = e^p$, $e_i^r = e^r$), $s_i = 0$, and

$$\frac{\partial s_i}{\partial e_i^p} = (1 - \tfrac{1}{n})f'(e^p), \qquad \frac{\partial s_i}{\partial e_i^r} = (1 - \tfrac{1}{n})g'(e^r).$$

Substituting gives

$$[b + \beta(1 - \tfrac{1}{n})]\,f'(e^p) = c'(e^p + e^r),$$ $$\beta(1 - \tfrac{1}{n})\,g'(e^r) = c'(e^p + e^r).$$

Since both sides equal $c'(e^p + e^r)$, stronger internal competition (higher $\beta$) increases $e^r$ and, by convex costs, decreases $e^p$. Larger $n$ reduces the marginal return to political effort through the $(1 - \tfrac{1}{n})$ term, but total waste $n e^r$ can remain large. Setting $\beta = 0$ removes politics entirely but sacrifices the company's ability to differentiate employees when $Y$ is the only (aggregate) signal.

There are other clever mechanisms for incentivizing employees to exert effort and to exert effort in the right direction, but in essence, these phenomena trade off with each other (for example, tournament theory incentivizes performance by comparing employees relatively, but causes selfishness and negative-sum competition). In other words, mechanisms to incentivize effort cause misdirected effort. This tradeoff is exacerbated by scale.

Volunteer's Dilemma

A lot of the important work of a small company is done on an unassigned or voluntary basis. This extends to challenging leadership, the internal status quo, and groupthink (ironically, this is what a startup is meant to do to the outside world).

Consider the following payoff matrix for two employees and a given voluntary task:

	Employee 2 Volunteers	Employee 2 Does Not Volunteer
Employee 1 Volunteers	$(b - c,\; b - c)$	$(b - c,\; b)$
Employee 1 Does Not Volunteer	$(b,\; b - c)$	$(0,\; 0)$

Where:

• $b > 0$ is the benefit provided to everyone if someone volunteers.
• $c > 0$ is the personal cost of volunteering.

For $n$ employees, the payoffs for a single employee can be modeled similarly but corresponding to the probability that no other employee volunteers or that at least one other employee volunteers. Say that the probability of another employee not volunteering is $p$ — we get a likelihood that no other employee volunteers equal to $p^{n-1}$ and a likelihood that at least one other employee volunteers equal to $1 - p^{n-1}$. To find our indifference point, we set the expected payoff of volunteering equal to the expected payoff of not volunteering:

$$b-c = b(1 - p^{n-1}) \quad\Rightarrow\quad p = \sqrt[n-1]{\frac{c}{b}}.$$

Since $b>c$, an employee's likelihood of not volunteering is higher the more employees there are, which is unsurprising. But the likelihood that no employee volunteers is therefore $p^n = (\frac{c}{b})^{\frac{n}{n-1}}$, which is also higher the more employees there are (and asymptotically approaches $\frac{c}{b}$). This means that as the team grows, even though there are vastly more candidates to volunteer for a given task, responsibility diffuses and the likelihood of that task being done drops. This is a massive cultural issue, where personal agency drops and pluralistic ignorance arises.

A Hard Rule To Follow

Evidence points so strongly toward the benefits of judicious hiring, yet most teams rush to hire nonetheless. Why?

The Wrong Reasons To Hire

These are the reasons I have seen organizations hire which most frequently backfire. They are also forces I have felt acting on me and have chosen to resist.

Hiring Confers Status

For most people outside of your company, a new hire is one of the most visible signals of your success. This in turn attracts more candidates and interest from investors, regardless of your mission, product, and business model. New hires also stroke your ego and the egos of anyone else to whom the new hire might report. It's common in the world of business to be asked how many "direct reports" you have, which is then used as a proxy for your importance.

This is part of a broader aspect of today's startup culture: building in public has evolved into celebrating the inputs of success rather than the outputs. Working "996", raising money, and hiring are all necessary steps towards success, but they are not the success itself. If you are truly mission-driven, neither is the revenue.

Hiring Feels Like Progress

Even aside from external validation and signaling, there is a natural internal pressure to hire. You know that to achieve any meaningful scale and growth, you will need to hire. It ends up on your checklist, rather than as a possible solution to the problem at hand. Your company ends up operating on a push rather than a pull mechanism and the modus operandi becomes hire to build to sell rather than build to solve a problem and hire to build the solution faster.

Venture Capital Encourages It

There is nothing wrong with accepting investment (we are proud to work with world-class investors at Assert), but it's important to understand its purpose and not allow it to cloud your judgment: in large, competitive markets, it is often worthwhile to focus on user adoption over profitability. Having to concern yourself with unit economics early on doesn't just mean slower adoption - it likely means next to no adoption. Moreover, securing capital can enable you to pay for top talent rather than lowering your standards.

Nonetheless, accepting investment encourages you to hire quickly, rather than thoughtfully. Because suddenly you can.

Founding Can Be Painful

It is uncomfortable to wander, let alone to do it on your own. Hiring quickly is an easy way to rush past that part.

The Right Reasons To Hire

These are the reasons I have seen organizations hire which are most frequently justified.

It's Hurting

Basecamp's hiring motto is "hire when it hurts". In other words, the default option is to not hire. When you encounter a bottleneck to the growth of the business, hiring can be considered as an option for remediation. Even in this case, however, you don't need to jump to hire.

Telegram, which reportedly earns over $1 billion in annual recurring revenue and has over a billion users, relies on a core engineering team of about 40 people. Its founder, Pavel Durov, emphasizes that one benefit of this leanness is automation: "when you intentionally don't allow some of your team members to hire more people to help them, they will be forced to automate things."

Many founders hire for competencies which they themselves lack. The problem with this is that you are likely to struggle at recruiting, assessing, and managing talent in those competencies. At Assert, we strive to hire for competencies we already have while teaching ourselves the skills we lack.

Opportunism

In addition to growing and cultivating a broad talent network, you may need to be persistent, patient, and pragmatic about the availability of that talent. People you know, let alone ones you don't, will enter the job market relatively stochastically and infrequently; they will exit it quickly. These windows might not line up with your exact needs and timelines and you should nonetheless move swiftly and decisively when outstanding candidates become available. You may be able to influence these windows, but not always.

Hypergrowth

Once you’ve found product–market fit, it’s only a matter of time before the world catches on. You’ve moved from exploration to exploitation, and speed becomes your advantage: you need to scale quickly. In this phase — especially for non-product functions like sales and marketing — it’s reasonable to hire ahead of immediate pain, playing the attrition game to build capacity before the constraint becomes visible.

Conclusion

As I've alluded to, there are great reasons to hire and any successful startup eventually needs to do so. But many founders hire to run away from themselves. "I can think. I can wait. I can fast." These are the words of Siddhartha, displaying his capacity for patience and planning. Great ventures begin with conviction, not headcount.